リスク管理最前線 第74回 〜オプション評価(パート1)二項モデル(前編)〜
- 欧米金融機関の現場から
- リスク管理コラム
- リスク管理最前線
オプション評価(パート1)二項モデル(前編)
今回から、オプション評価の手法についてご紹介したいと思います。オプション評価にはいくつものモデルが存在し実用化されていますが、今回はその中でも基本的な二項モデル(バイノミアル・モデル)を取り上げます。1979年にコックス、ロス、ルービンシュタインによって提唱されたモデルであるため、3名の頭文字をとって「CRRモデル」とも呼ばれています。基本的なモデルですが、直感的に理解しやすく、またアメリカン・オプション等満期までの原資産の価格経路に価値が依存するオプションの評価にも用いることができるため、実務的に幅広く利用されています。
1ステップ・ツリー
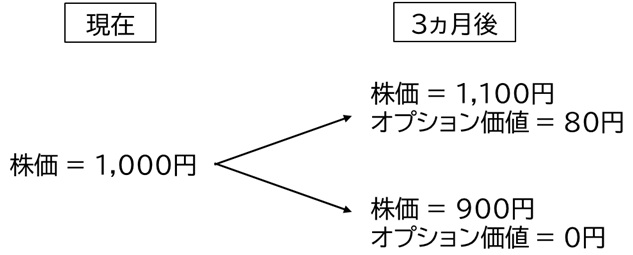
株式価格を例にモデルを説明いたします。非現実的な単純化ではありますが、現在株価1,000円の株式Aが、3ヶ月後に10%上昇か10%下落かのどちらかだと仮定します。すなわち株価は1,100円か900円のいずれかになるとします。また、その間の配当はないものとします。
この株式Aを原資産とする満期3ヶ月の行使価格1,020円のコールオプションを考えます。このオプションの買い手は、3ヶ月後に株価が1,100円に上昇すれば権利を行使し、1,100円 – 1,020円 = 80円の利益を得ます。一方で、株価が900円に下落すれば権利を行使せず、利益は0円です。【図74-1】はこの例における株価とオプションペイオフの関係を表したものです。
【図74-1】株価と行使価格1,020円のコールオプションの価値
裁定機会がない前提
オプション評価にあたって、市場が合理的で「裁定機会がない」という前提をおきます。裁定機会がないという前提を簡単に表現すると、リスクゼロで、無資金で、確実に利益が得られる機会、いわゆる「フリーランチ」がない状態です。
別の視点では、2つのポートフォリオが、将来時点で、どのような状況下でも、同一のキャッシュフローの場合、2つのポートフォリオの現在価値は等しくなければなりません。なぜなら、もし価格が異なる場合には、価格の高い方のポートフォリオを売って、価格が低い方のポートフォリオを買えば、今日時点でその差額を手にすることができ、将来時点においては2つのポートフォリオのキャッシュフローが相殺され、何らキャッシュフローが発生しないため、裁定取引が成立してしまうからです。
実際の市場では取引コストが発生し、取引単位や取引時間等様々な制約がある場合が多く、必ずしも合理的ではないため、裁定機会が生じる場合もありますが、多数の参加者がいる市場では裁定機会はすぐ是正されてしまうので、裁定機会がないという前提は理にかなっていると言えます。
株式とコールオプションによる無リスクポートフォリオの複製
上記の例で、株式AをΔ単位買い持ちし、コールオプションを1単位売るポートフォリオを構築します。3ヶ月後に株価が1,100円に上昇すると、このポートフォリオの価値は (1,100円×Δ単位–80円×1単位) となります。逆に株価が900円に下落すると、このポートフォリオの価値は (900円×Δ単位–0円×1単位) となります。
もし、1,100×Δ–80=900×Δが成り立つ場合、このポートフォリオは3ヶ月後の株価にかかわらず常に同じ価値を持つということになります。この数式を解けばΔ=0.4の時に等式が成立し、その時3ヶ月後のポートフォリオ価値は360円であることがわかります。
次に、3ヶ月後に常に360円の価値があるポートフォリオの現在価値は、無リスク金利で割り引くことができ、3ヶ月間の無リスク金利(リスク・フリー・レート)が連続複利ベースで年利2%の場合、358.2 (=360×e-2%×0.25)となります。
コールオプションの現在価値を C円 とすると、ポートフォリオの現在価値は1,000円×0.4単位–C円と表され、裁定機会がない前提から400–C=358.2が成立し、C=41.8円と求められます。
株価の上昇確率とオプション価値
ここまでの議論でお気づきになられたかと思いますが、二項モデルにおいてオプションの価値を求めるのに必要な情報は3ヶ月後に上昇した場合の株価と下落した場合の株価と、無リスク金利だけです。すなわち株価の上昇確率、下落確率はオプションの現在価値には影響しません。
一見、株価の上昇確率が高ければコールオプションの価値も高いのではないかと思われるかもしれませんが、上昇確率は現在の株価に織り込まれるため、現在の株価を所与としたオプション価値には影響がないと考えれば理解しやすいと思います。誤解のないように補足しますと、オプション取引後に株価が変動すればそのオプションの価値も都度変動します。
1ステップ・ツリーの一般化
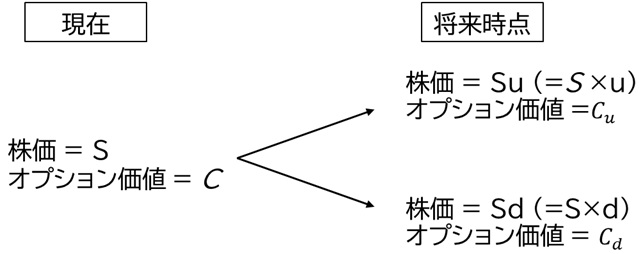
先の例を一般化した形で示したものが【図74-2】です。
【図74-2】一般化した株価とコールオプションの価値
Δ=(Cu−Cd)/S(u−d)
(74.1)
として、株式をΔ単位、オプションを-1単位保有するポートフォリオを想定します。将来時点において、
株価がSuとなった場合の価値は、
Su∆−Cu=Su(Cu−Cd)/S(u−d)−Cu=(Cud−Cdu)/(u−d)
株価がSdとなった場合の価値は、
SdΔ−Cd=Sd (Cu−Cd)/S(u−d)−Cd= (Cud−Cdu)/(u−d)
となり、いずれの場合も価値が等しくなります。
したがって、このポートフォリオの現在価値は無リスク金利r、期間tで割り引くことにより求められるため、
SΔ−C=(Cud−Cdu)/(u−d)e-rt
(74.2)
が成立します。(74.1)式を(74.2)式に代入すると、オプション価値Cは、
C=Cu[(1−de-rt)/(u−d)]+Cd[(ue-rt−1)/(u−d)]
(74.3)
と求められます、(74.3)式を変形すると、
C=e-rt[pCu+(1−p)Cd]
(74.4)
ただし、
p=(ert−d)/(u−d)
(74.5)
となります。
やや数式が多くなりましたが、(74.4)式を見ると、あたかも満期時点のオプション価値を株価の上昇確率pで重み付けして、無リスク金利で割り引くことにより、オプションの現在価値を求めているかのようです。この点については次回さらに議論を深めていきたいと思います。
【参考文献】
・Valuation and Risk Models: Global Association of Risk Professionals 等
◇MRAフェロー 伊東啓介
リスク管理最前線 第73回 〜債券市場分析(パート5)債券ポートフォリオのリスク指標〜
リスク管理最前線 第72回 〜債券市場分析(パート4)イールドカーブ実務編 作成時の実務上の留意点と債券市場への応用〜
リスク管理最前線 第71回 〜債券市場分析(パート3)イールドカーブ実務編 インターバンクレートの使用〜
リスク管理最前線 第70回 〜債券市場分析(パート2)複利、パーレート、フォワードレート〜
リスク管理最前線 第69回 〜債券市場分析(パート1)スポットレートとディスカウントファクター、イールドカーブ〜
リスク管理最前線 第68回 〜「ロードス島攻防記」に見る聖ヨハネ騎士団の戦略とリスク管理〜
リスク管理最前線 第67回 〜ストレステスト実践編〜
リスク管理最前線 第66回 〜オペレーショナルリスク〜
リスク管理最前線 第65回 〜信用リスクの定量化〜
リスク管理最前線 第64回 〜カントリーリスク〜
リスク管理最前線 第63回 〜信用格付(その2)〜
リスク管理最前線 第62回 〜信用格付(その1)〜
リスク管理最前線 第61回 〜ボラティリティの推定(その2)〜
リスク管理最前線 第60回 〜ボラティリティの推定(その1)〜
リスク管理最前線 第59回 〜統計分析を活用した金利リスクのヘッジ手法〜
リスク管理最前線 第58回 〜多変量相関のモデリング コピュラ〜
リスク管理最前線 第57回 〜金融市場におけるコリレーションの特性〜
リスク管理最前線 第56回 〜コリレーション・リスク〜
リスク管理最前線 第55回 〜バリュー・アット・リスク(VaR)モデルに関するその他の論点〜
リスク管理最前線 第54回 〜バリュー・アット・リスク(VaR)マッピング〜
リスク管理最前線 第53回 〜バリュー・アット・リスク(VaR)モデルのバックテスト〜
リスク管理最前線 第52回 〜市場リスク指標の推定(パート5)テール・リスク定量化の統計学的アプローチ〜
リスク管理最前線 第51回 〜市場リスク指標の推定(パート4)ノンパラメトリック手法の利点と欠点〜
リスク管理最前線 第50回 〜市場リスク指標の推定(パート3)ヒストリカル・シミュレーション法の改善手法〜
リスク管理最前線 第49回 〜市場リスク指標の推定(パート2)期待ショートフォールの推定とリスクデータの初期検証〜
リスク管理最前線 第48回 〜市場リスク指標の推定(パート1)損益・利益率データの生成とVaR〜
リスク管理最前線 第47回 〜統合型リスクマネジメント (ERM) (パート2)〜
リスク管理最前線 第46回 〜統合型リスクマネジメント (ERM) (パート1)〜
リスク管理最前線 第45回 〜データ統合とリスクレポーティング〜
リスク管理最前線 第44回 〜信用リスクの移転手法〜
リスク管理最前線 第43回 〜リスク管理のガバナンス(パート5)リスクのモニタリングと部署間の連携〜
リスク管理最前線 第42回 〜リスク管理のガバナンス(パート4)リスクアペタイトとリミット〜
リスク管理最前線 第41回 〜リスク管理のガバナンス(パート3)取締役会の役割〜
リスク管理最前線 第40回 〜リスク管理のガバナンス(パート2)〜
リスク管理最前線 第39回 〜リスク管理のガバナンス(パート1)〜
リスク管理最前線 第38回 〜リスク管理ロードマップ(パート4)リスクアペタイトの実践〜
リスク管理最前線 第37回 〜リスク管理ロードマップ(パート3)リスク管理運用態勢の構築とリスクリミット体系〜
リスク管理最前線 第36回 〜リスク管理ロードマップ(パート2)リスクのマッピングと戦略の選択〜
リスク管理最前線 第35回 〜リスク管理ロードマップ(パート1)リスク・アペタイトの設定〜
リスク管理最前線 第34回 〜リスクの合算と統合型リスク管理〜
リスク管理最前線 第33回 〜リスクの定量化指標〜
リスク管理最前線 第32回 〜リスクの認識〜
リスク管理最前線 第31回 〜リスクの類型と相互関連(パート2)〜
リスク管理最前線 第30回 〜リスクの類型と相互関連(パート1)〜
リスク管理最前線 第29回 〜バリュー・アット・リスク実践編 モンテカルロ・シミュレーション法〜
リスク管理最前線 第28回 〜バリュー・アット・リスク実践編 ヒストリカル・シミュレーション法〜
リスク管理最前線 第27回 〜バリュー・アット・リスク実践編 分散共分散法〜
リスク管理最前線 第26回 〜リスク管理態勢強化と独立したリスク管理部署の重要性〜
リスク管理最前線 第25回 〜コモディティ市場のリスク管理(パート2)〜
リスク管理最前線 第24回 〜コモディティ市場のリスク管理(パート1)〜
リスク管理最前線 第23回 〜株式市場のリスク管理(パート2)〜
リスク管理最前線 第22回 〜株式市場のリスク管理(パート1)〜
リスク管理最前線 第21回 〜英国の新型コロナウィルス対策に見るリスク管理の考え方〜
リスク管理最前線 第20回 〜外国為替(FX)のリスク管理〜
リスク管理最前線 第19回 〜債券市場のリスク管理〜
リスク管理最前線 第18回 〜金利オプション取引の活用によるリスク管理〜
リスク管理最前線 第17回 〜金利市場リスク(パート3)〜
リスク管理最前線 第16回 〜金利市場リスク(パート2)〜
リスク管理最前線 第15回 〜金利市場リスク(パート1)〜
リスク管理最前線 第14回 〜流動性リスク(パート2)〜
リスク管理最前線 第13回 〜流動性リスク(パート1)〜
リスク管理最前線 第12回 〜ソルベント・ワインドダウン(円滑な業務撤退)計画の作成〜
リスク管理最前線 第11回 〜自己資本充実度の評価(パート2)〜
リスク管理最前線 第10回 〜自己資本充実度の評価(パート1)〜
リスク管理最前線 第9回 〜ストレス・テスト(パート2)〜
リスク管理最前線 第8回 〜ストレス・テスト(パート1)〜
リスク管理最前線 第7回 〜バリュー・アット・リスク(パート2)〜
リスク管理最前線 第6回 〜バリュー・アット・リスク(パート1)〜
リスク管理最前線 第5回 〜リスク・リミットの設定と管理(パート2)〜
リスク管理最前線 第4回 〜リスク・リミットの設定と管理(パート1)〜
リスク管理最前線 第3回 〜リスク管理フレームワーク(枠組み)の構築〜
リスク管理最前線 第2回 ~まずはリスクアペタイトありき~
リスク管理最前線 第1回 ~なぜリスク管理が必要か?~
