リスク管理最前線 第65回 〜信用リスクの定量化〜
- リスク管理コラム
- リスク管理最前線
- 欧米金融機関の現場から
信用リスクの定量化
市場リスクの定量化手法については、代表的なバリュー・アット・リスク(VaR)等の手法を本コラムでも紹介してきました。信用リスクの定量化についても同様のアプローチが考えられますが、市場リスクの対象となる金融商品には一般的に市場価格が存在し、そのヒストリカルデータも取得できるのに対して、信用リスクの対象となるローン等の与信に関しては市場価格が明らかでないため、VaR算出の代表的な手法であるヒストリカル・シミュレーション法の適用が困難です。また、信用リスクの特性として、基本的に満期で元本額が返済され、デフォルト時にのみ回収額が大きく毀損するため、損失額の分布が市場リスクとは異なります。今回はまずエコノミックキャピタル(リスク資本)の概念をご説明してから、ややテクニカルな内容となりますが、信用リスクの代表的な定量化手法の概要をご紹介します。
エコノミックキャピタル
エコノミックキャピタル(Economic Capital)とは、企業経営において生じるリスクをカバーするために必要なリスク資本の総額です。また、規制資本(Regulatory Capital)とは、金融機関が金融監督当局の要請に基づいて保有すべき最低限の資本のことを指し、金融機関は経営の安全性の確保のために、自己資本をエコノミックキャピタルや規制資本以上に保つことが求められています。金融機関以外の事業会社においても、経営の安全性の確保は同様に重要であり、エコノミックキャピタルを把握し、自己資本を充足させることが望ましいと言えます。
信用リスクにかかるエコノミックキャピタルの考え方は、ポートフォリオの一定期間内の信用リスク損失額がエコノミックキャピタルを超過する確率を一定レベル以下に抑えるという目的のもと、例えば1/1000以下に抑える場合、信用リスク損失分布の99.9パーセンタイルに相当する金額をエコノミックキャピタルとして設定することになります。厳密には予想損失額相当分に引当金が計上されている場合、予想損失額を超過する損失に相当する額がエコノミックキャピタルとなります。(下図「信用リスク損失分布とエコノミックキャピタルの関係」参照)
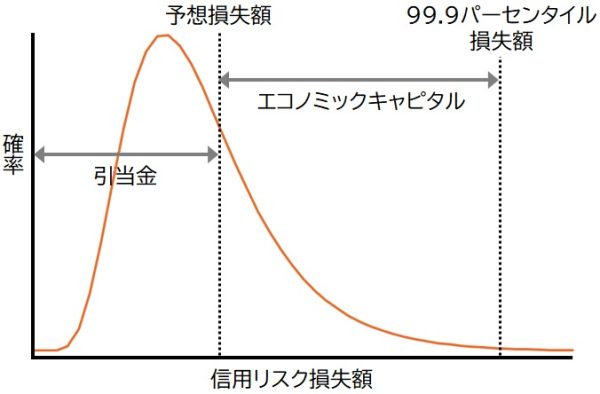
【信用リスク損失額の分布とエコノミックキャピタルの関係】
代表的な信用リスク定量化モデル
代表的な信用リスクの定量化モデルとして、信用リスク損失割合の標準偏差、正規コピュラ(Gaussian Copula)を応用したバシチェック・モデル(Vasicek)、クレジットメトリックス(Credit Metrics)の3つがあげられます。以下各モデルの概要についてご紹介します。
信用リスク損失割合の標準偏差
各ローンの元本額、デフォルト確率、回収率、ローン間のデフォルト相関係数から、ポートフォリオの信用リスク損失割合の標準偏差を求めるものです。単純化のため、全てのローンの元本額、回収率、ローン間のデフォルト相関係数が等しい場合、信用リスク損失割合の標準偏差は下式のとおりとなります。
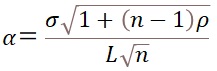
(65.1)
ここで、
![]()
(65.2)
ただし、
α: ポートフォリオの信用リスク損失割合(パーセンテージ損失)の標準偏差
σ: 各ローンの信用リスク損失額の標準偏差
n: ポートフォリオ内のローンの数
L: ローンの元本額
ρ: ローン間のデフォルト相関係数
PD : 各ローンのデフォルト確率
R: 各ローンのデフォルト時の回収率
ポートフォリオの信用リスク損失額の分布は、ポートフォリオ内のローン間のデフォルトの相関に影響を受けます。(65.1)式の示唆は、相関係数が大きいほど信用リスク損失割合の標準偏差(バラツキ)が大きくなるという点です。概念的には、相関が高いほど多くのローンが同時期にデフォルトする可能性が高くなり、損失額の分布の裾野が広がる、すなわちリスクも大きくなると考えることができます。
リスク管理の実務においては標準偏差より、分布の裾野である99.9パーセンタイル値等のテールリスクに関心がありますが、損失分布が正規分布ではないため、テールリスクを標準偏差から求めることができません。パーセンタイル値の推定については後述の手法が用いられます。
バシチェック・モデル
バシチェック・モデルは正規コピュラを活用したモデルで、解析的にポートフォリオのデフォルト率のパーセンタイル値を求める手法です。この手法は金融監督当局が規制資本を決定する際に用いられています。
コピュラについては本コラムでもご紹介しましたが、コピュラの利点は複雑な多変量の分布関数を、各変数の分布関数とそれらの依存関係に分解することにより、数学的な取り扱いが単純化できるところにあります。正規コピュラでは各ローンの信用リスクを標準正規分布に置き換え、あるパーセンタイル値(閾値)を超えるとデフォルト発生とみなします。さらに単純化のため、与信先間の信用リスクの相関係数は全て同一の値と仮定する1ファクターの相関モデルが用いられます。結論だけ示すと、ローンの数が十分に大きいポートフォリオの場合、デフォルト率のパーセンタイル値は下式のとおりとなります。
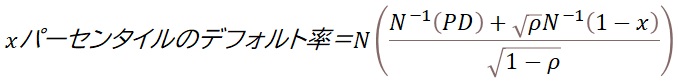
(65.3)
ただし、
N: 正規分布の累積分布関数
N-1: 正規分布の累積分布関数の逆関数
ρ: ローン間のデフォルト相関係数
PD : 各ローンのデフォルト確率(共通)
(65.3)式の示唆は、やはり相関係数が大きいほどデフォルト率のパーセンタイル値が大きくなる、すなわち信用リスクが大きくなると言う点です。
xパーセンタイルのデフォルト率を最大デフォルト率と読み換えると、エコノミックキャピタルは以下の式で算出できます。
![]()
(65.4)
ただし、
PD : 各ローンの平均デフォルト確率(共通)
LGD: 1 – 回収率
EAD: デフォルト時のエクスポージャー(=ローン元本額の合計)
クレジットメトリックス
クレジットメトリックスは本コラムの信用格付の回でご紹介した格付の遷移確率、すなわち格付毎の1年後に遷移している各格付の確率を表した格付遷移行列を利用した手法で、モンテカルロ・シミュレーションにより信用リスク損失額の分布を生成する手法です。この手法は実際に金融機関が内部モデルでエコノミックキャピタルを算出する際に用いられています。
この手法ではモンテカルロ・シミュレーションの各試行において、ローン間の信用リスク遷移の相関を考慮した多変量の乱数を発生させ、全てのローンの格付遷移を時系列的にシミュレーションすることにより、一定期間後の信用リスク損失額のサンプルを生成します。そして試行を繰り返すことにより信用リスク損失額の分布を生成し、設定したパーセンタイル値の損失額をエコノミックキャピタルとします。
最後になりますが、いずれのモデルにおいても、パラメーターの推定は必ずしも容易ではなく、モデル自体も単純化されたものであるため、正確性には限界があることを認識して取り扱う必要があります。
【参考文献】
・Valuation and Risk Models: Global Association of Risk Professionals
・日本銀行金融機構局金融高度化センター 内部格付制度と信用リスク計量化 等
◇MRAフェロー 伊東啓介
