リスク管理最前線 第70回 〜債券市場分析(パート2)複利、パーレート、フォワードレート〜
- リスク管理最前線
- 欧米金融機関の現場から
- リスク管理コラム
債券市場分析(パート2)
複利、パーレート、フォワードレート
前回は債券市場分析の基礎となるディスカウントファクターカーブあるいはイールドカーブの作成方法について簡単な例を用いてご紹介しました。ディスカウントファクターとスポットレートは、一方から、もう一方を導出できるため、実務的にはディスカウントファクターカーブを基礎データとして金利市場や債券市場の分析を行います。
視覚的にはイールドカーブは縦軸にスポットレート、横軸に期間をプロットしたもの、ディスカウントファクターカーブは縦軸にディスカウントファクター、横軸に期間をプロットしたもので、通常曲線になることから「カーブ」という名称が使用されています。
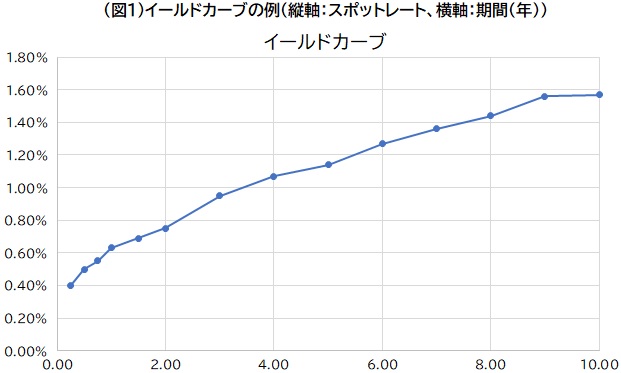
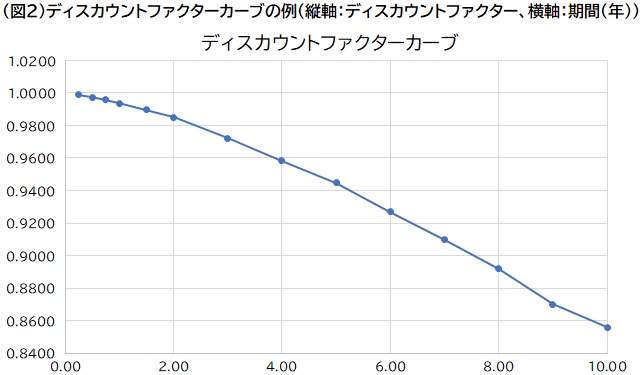
今回は、複利の概念、それからパーレート、フォワードレート、およびこれらとスポットレートの関係性についてご紹介します。
複利
前回ディスカウントファクターとスポットレートについて下記の関係式を示しました。
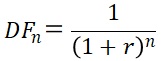
(70.1)
ただし
DFn : 期間n年のディスカウントファクター
r : スポットレート(1年複利)
右辺の分母に注目すると、指数が年数のべき乗となっていますが、これはスポットレートに1年ごとの複利を想定していることになります。複利とは一定期間後に得られた利息を元本に組み入れて、次の期間の利息計算の元本とする計算方法です。
例えばスポットレートに半年ごとの複利を想定すると、(70.1)式は下記のように書き換えられます。
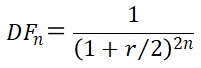
(70.2)
ただし
DFn : 期間n年のディスカウントファクター
r : スポットレート(半年複利)
さらに運用期間を限りなく短くした場合の複利を連続複利と呼び、ディスカウントファクターと連続複利の間には、自然対数で表現される下記の関係式が成立します。
![]()
(70.3)
ただし
DFn : 期間n年のディスカウントファクター
r : スポットレート(連続複利)
複利の運用単位の期間が異なると、同じ金利で同じ期間運用しても運用リターンは異なります。一般的には図3のとおり、複利の運用単位の期間が短くなればなるほど、運用リターンは高まります。これは利息を効果的に再運用できるからです。
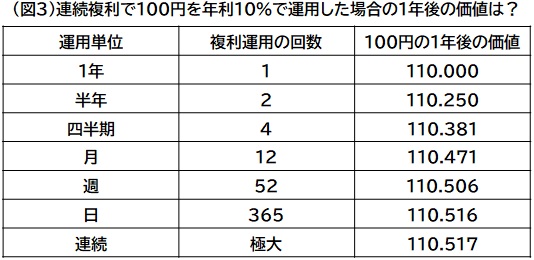
これらが示す通り、ある期間に対応するディスカウントファクターは一つの値ですが、金利についてはその定義によって数値が変わってきます。実務的にディスカウントファクターが基礎データとして用いられている大きな理由はここにあります。
パーレート
パーレートとは、債券のキャッシュフローの現在価値がちょうど額面と等しくなる債券の利率のことです。
例えばパーレート(年利ベース)をP% とすると、満期までT年、額面100円、年2回利払いの利付債券においては、下式が成立します。
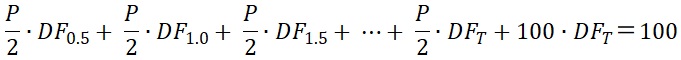
(70.4)
債券ではありませんが、金利スワップは一定期間変動金利(以前、金利スワップの指標金利はLibor (ロンドン市場において銀行間で取引される短期金利)が中心でしたが、廃止となったため、現在は米国ではSOFR、日本ではTIBOR等が指標金利として使用されています。)と、スワップレートと呼ばれる固定金利を交換する金利デリバティブ取引で、その市場規模は債券市場を凌ぎますが、スワップレートは、まさにパーレートそのものです。
フォワードレート
フォワードレートは、現在のスポットレートから導かれる、将来時点のスポットレートのことです。
例えば現在の1年スポットレートが1%、2年スポットレートが2%の場合、1年先の1年フォワードレートをFとすると、現時点から2年間スポットレートで運用したリターンと、現時点から1年間スポットレートで運用後、さらに1年後から1年間フォワードレートで運用した時の合計リターンは、市場裁定が働くことを前提とすると等しくなるので、スポットレートが1年複利の場合、
![]()
が成立します。これを変形して、
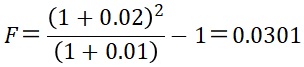
とFが求められます。直感的には2年間2%で運用するのと、1年目1%、2年目3%(平均2%)で運用した結果がほぼ等しくなると考えればこの結果は分かりやすいと思います。
より一般的に、m時点からn時点 (m < n) のフォワードレートFmnは、期間mのスポットレートrmおよび期間nのスポットレートrnを用いて下式のように求められます。(1年複利の場合)
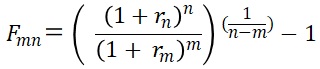
(70.5)
さらに(70.5)式に、(70.1)式を代入すると、m時点からn時点のフォワードレートFmnは期間mのディスカウントファクターDFmおよび期間nのディスカウントファクターDFn用いて下式のように求められます。
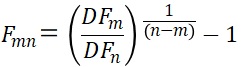
(70.6)
スポットレートとパーレート、フォワードレートの大小関係
最後に同じ満期のスポットレートとパーレート、さらに同じ満期をスタート時点とするフォワードレートの大小関係についてですが、これはイールドカーブの形状によります。
イールドカーブがフラット(全ての期間のスポットレートが同じ)の場合、パーレートとフォワードレートも全てスポットレートと同じになります。
イールドカーブが右肩上がり(期間が長いほどスポットレートが大きい)場合、
フォワードレート > スポットレート > パーレート
の関係が成立し、
イールドカーブが右肩下がり(期間が長いほどスポットレートが小さい)場合、
フォワードレート < スポットレート < パーレート
の関係が成立します。
【参考文献】
・Valuation and Risk Models: Global Association of Risk Professionals
・スポットレートとその応用(日本銀行金融機構局金融高度化センター)等
◇MRAフェロー 伊東啓介
