リスク管理最前線 第61回 〜ボラティリティの推定(その2)〜
- 欧米金融機関の現場から
- リスク管理コラム
- リスク管理最前線
ボラティリティの推定(その2)
今回は前回に引き続きボラティリティについて、まず指数加重移動平均法(指数平滑化法)の拡張版と言えるGARCHモデルについてご紹介します。さらにインプライド・ボラティリティ、コリレーションの推定についても触れます。
GARCHモデル
時系列データのボラティリティをモデル化する別の手法としてGARCHモデルがあります。GARCH(1,1) によるボラティリティのモデル化は下式のとおりです。
![]()
(61.1)
ただし、
VL : 日次リターンの分散の長期的平均値
α, β, γ : 各構成要素の重み付け。それぞれ0から1の間の値。和は1になる。
指数加重移動平均法との違いは長期的平均値がパラメーターとして設定されていることです。なおγ=0の場合、(61.1)式は、前回ご紹介した指数加重移動平均法(指数平滑化法)の推定式((60.8)式)と同じになり、指数加重移動平均法(指数平滑化法)はGARCH(1,1)モデルにおいて平均回帰性がない、特別の場合と言えます。
平均回帰
αとβの意味合いについては前回指数加重移動平均法のλの推定のところで触れましたが、γについては長期的平均値に回帰する程度と言え、γが大きいほど長期的平均値に引っ張られる「平均回帰」の傾向が強まります。全てのものに平均回帰性があるわけではないのですが、ボラティリティに関しては経験的に平均回帰性があります。ボラティリティは長期的には低い状況も、高い状況も、ずっとは続かず、上下動する場合が多いと言えます。他に平均回帰性がある代表的なものには金利が挙げられます。
長期間のボラティリティ
これまで日次リターンのボラティリティを中心に説明を続けてきましたが、日次よりも長期間のボラティリティを予測したい場合もあります。ボラティリティが一定の世界においては、分散は時間に比例する、すなわちボラティリティは時間の平方根に比例すると考えられます。例えばT日間のVaRは日次VaRの√T倍となると推定されます。
しかしボラティリティの平均回帰性を考慮する場合にはこの考え方に修正が必要です。もし現在ボラティリティが長期的平均水準より低い状況の場合、今後ボラティリティが上昇する可能性が高くなるため、T日間のボラティリティを日次ボラティリティの√T倍とすると、リスクを過小評価する結果となります。
GARCH(1,1)モデルにおいて、t日後におけるボラティリティは下記の式で推定されます。
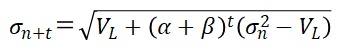
(61.2)
(61.2)式において、α+β<1であることから、tが大きいほど、t日後の推定ボラティリティが長期的平均に収束する傾向があることが分かります。
インプライド・ボラティリティ
インプライド・ボラティリティとは、オプションの市場価格からモデルで逆算されるボラティリティのことです。オプション価格が高くなるとインプライド・ボラティリティも上昇します。インプライド・ボラティリティは将来の変動予想に関するものですが、これに対して、指数加重移動平均法やGARCHモデルで推定されたボラティリティは過去データから求められたものであり、ヒストリカル・ボラティリティと呼ばれます。
リスク指標は将来の予測に関するものであり、同じく将来の変動予測に関するインプライド・ボラティリティの方が、ヒストリカル・ボラティリティよりもリスク指標の推定に適していることが実証されています。1ヶ月後の予想には1ヶ月満期の、3ヶ月後の予想には3ヶ月満期のオプションのインプライド・ボラティリティを参照することが妥当です。また、ボラティリティは一定でないため、満期の異なるオプションのインプライド・ボラティリティは通常それぞれ異なります。
オプション市場が存在しない、あるいは存在しても流動性が極めて低い場合には、インプライド・ボラティリティは観測できませんが、リスク管理において、可能な場合には常にヒストリカル・ボラティリティのみならずインプライド・ボラティリティにも着目する必要があります。
なお、インプライド・ボラティリティの代表的な指標として、経済ニュース等でも取り上げられるVIX指数があります。VIX指数は米国の代表的な株価指数の一つであるS&P500の30日間オプションのインプライド・ボラティリティを元に算出されています。
コリレーションの推定
リスク管理において、コリレーションの推定も重要ですが、これにはボラティリティ推定と同様の手法を適用することができます。分散からボラティリティを推定するのと同様に、共分散からコリレーションを推定するアプローチです。指数加重移動平均法による共分散の推定は下式のとおりです。
![]()
(61.3)
ただし、
covn: 日付nにおける資産Xと資産Yの推定共分散
xn-1,yn-1 : それぞれ日付n-1における資産Xと資産Yのリターン
λ : 指数加重移動平均法のウェイトの逓減速度のパラメーター
(61.3)式は、前回ご紹介した分散の推定式である(60.8)式と似ています。XとYの共分散はXの標準偏差(ボラティリティ)及びYの標準偏差(ボラティリティ)と相関係数(コリレーション)を掛け合わせたものですので、XとYの共分散、Xのボラティリティ、Yのボラティリティの推定値からXとYのコリレーションを算出することができます。注意点としてはXとYの共分散及びXのボラティリティ、Yのボラティリティの推定にあたっては、共通のλの値を採用する必要があります。
【参考文献】
・Valuation and Risk Models: Global Association of Risk Professionals 等
◇MRAフェロー 伊東啓介
