リスク管理最前線 第48回 〜市場リスク指標の推定(パート1)損益・利益率データの生成とVaR〜
- 欧米金融機関の現場から
- リスク管理コラム
- リスク管理最前線
市場リスク指標の推定(パート1)損益・利益率データの生成とVaR
今回から市場リスク指標の推定(定量化)に関するトピックスをご紹介したいと思います。今回は代表的な市場リスク指標であるバリュー・アット・リスク(以下「VaR」)の推定やVaRのバックテストに必要となる損益や利益率のデータの生成と、VaRの代表的な推定方法についてです。
損益データ
ある資産(またはポートフォリオ)の期間 t の損益は、期間tにおける時価の変化に、同期間に発生した利払いや配当等のキャッシュフローを加えたものとなります。なおプラスであれば利益、マイナスであれば損失ということになります。
![]() (48.1)
(48.1)
ただし、
RLt:期間 t( t-1 時点から t 時点まで)の損益
Pt:t 時点の資産の時価
Pt-1: t-1 時点の資産の時価
Dt:期間 t に資産から発生した利払いや配当等のキャッシュフロー
より厳密には、t と t-1 で時点が異なるため、キャッシュの時間的価値を考慮する必要があり、 t-1 を現在、t を将来時点とすると、
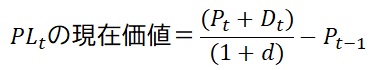
(48.2)
![]()
(48.3)
ただし、
d:期間 t の割引率
注)簡略化のため Dt は t 時点に発生したものとみなす
と表されますが、通常損益は日次で把握され、その場合期間 t は短く、割引率が十分小さくなり、簡略化のため割引率が無視され、(48.1)の式が実務的に損益データとして用いられています。
利益率データ
上記損益データの定義を用いると、期間tの利益率は、単利(算術リターン)では、
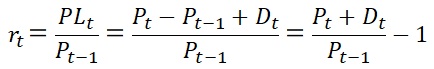
(48.4)
ただし、
rt:期間 t における単利(算術リターン)
と表され、期間 t の損益を t-1 時点の資産価値で割ったものとなります。
また連続複利(幾何リターン)では、同期間の利益率は、
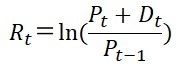
(48.5)
ただし、
Rt:期間 t における連続複利(幾何リターン)
と表されます。
リスク管理の実務において資産価格あるいは損益のシミュレーションを行う際には連続複利(幾何リターン)が使用されることが多いのですが、それにはいくつかの理由があります。まず連続複利では資産価値が負にならないことが担保されるので、シミュレーション結果がより現実的なものとなります。またある期間を細分化した場合、細分化した各期間の連続複利の合計が、その期間全体の連続複利となることから、数学的に扱いやすいという点もあります。
なお単利と複利は期間が短く利益率が小さい場合には近い値になりますが、長期間の利益率を考慮する場合には大きな違いが生じることがあります。これは複利においては、期間中発生したキャッシュフローの再運用が考慮されるからですが、特に長期間の利益率を考慮する場合には複利の考え方がより現実的だと言えます。
VaRの推定
VaRの推定については、過去に本コラムでも何度か取り上げていますが、ここでは代表的なVaR推定手法である、ヒストリカル・シミュレーション法、パラメトリック法、およびモンテカルロ・シミュレーション法の概要を簡単に振り返ります。
ヒストリカル・シミュレーション法
比較的シンプルで実務的に最も使用されているのが、ヒストリカル・シミュレーション法です。この手法は、現在の資産(またはポートフォリオ)価値に、過去観察された利益率データを適用することにより、損益データのサンプルを多数作成し、損失の大きい順に並べることでVaRを推定する手法です。
例えば1,000個の損失データサンプルがあり、95%信頼水準のVaRを求める場合、VaRを超える損失が発生する確率が5%なので、50個のデータがVaRより大きくなることから、損失の大きい順にサンプルを並べた51番目のサンプルの損失額がVaRになります。Excelのデータセットの場合、LARGE関数やPERCENTILE関数を使用して、特定の信頼水準のデータを求めることができます。
パラメトリック法
これは資産の損益や利益率の元データが、ある統計的な分布に従うと仮定して、その分布から統計的手法によりVaRを推定するアプローチで、まずは統計的な分布を元データにフィッティングすることから始まります。ヒストリカル・シミュレーション法と比較すると、統計的分布のパラメーター推定というステップが加わりますが、統計学的に取り扱いやすくなるというメリットがあります。パラメトリック法にはいくつかのモデルがあります。
① 損益が正規分布に従うモデル
![]()
(48.6)
ただし、
α:VaRの信頼水準(例えば95%)
zα:α に対応する標準正規変量(例えばα=95%の場合1.645、α=95%の場合2.326)
μ:VaRの対象期間の損益の推定平均
σ:VaRの対象期間の損益の推定標準偏差
② 単利(算術リターン)が正規分布に従うモデル
![]()
(48.7)
ただし、
α:VaRの信頼水準(例えば95%)
zα:α に対応する標準正規変量(例えばα=95%の場合1.645、α=95%の場合2.326)
μr:VaRの対象期間の単利(算術リターン)の推定平均
σr:VaRの対象期間の単利(算術リターン)の推定標準偏差
Pt-1:t-1 時点の資産の時価
③ 連続複利(幾何リターン)が正規分布に従うモデル
![]()
(48.8)
ただし、
α:VaRの信頼水準(例えば95%)
zα:αに対応する標準正規変量(例えばα=95%の場合1.645、α=95%の場合2.326)
μR:VaRの対象期間の連続複利(幾何リターン)の推定平均
σR:VaRの対象期間の連続複利(幾何リターン)の推定標準偏差
Pt-1:t-1 時点の資産の時価
なおこのモデルにおいて、幾何リターンが正規分布に従うという前提は、資産価値及びVaRが対数正規分布に従うということを意味しており、資産価格が負にならないため、前述のとおりリスク管理の実務で広く利用されています。株式等のオプション価格の算出に使用されるブラック・ショールズ・モデルもこの前提に基づいています。
モンテカルロ・シミュレーション法
パラメトリック法で推定した損益あるいは利益率の確率変動モデルや、さらに複雑化したモデルにおいて、標準正規乱数等を発生させることにより、資産価格推移および損益のサンプルデータを生成することが可能です。モンテカルロ・シミュレーション法は、このシミュレーションを多数試行することにより損失の分布を作成し、VaRを推定する手法です。資産価格の分布、確率過程、資産価格間の相関等に関して、モデルの自由度から、資産の特性に応じた多様な設定が可能であり、強力な手法です。
【参考文献】
Market Risk Management and Measurement (Pearson Education) 他
◇MRAフェロー 伊東啓介
