リスク管理最前線 第60回 〜ボラティリティの推定(その1)〜
- 欧米金融機関の現場から
- リスク管理コラム
- リスク管理最前線
ボラティリティの推定(その1)
今回はボラティリティが一定ではなく、時とともに変動するものであることを踏まえたうえで、ボラティリティの一般的な推定方法および指数加重移動平均法(指数平滑化法)についてご紹介します。さらにヒストリカル・シミュレーションへの応用について触れます。
資産リターンの正規分布からの乖離
ボラティリティがもし一定であれば、株式や商品の一定期間の資産のリターンの分布は正規分布に近づきます。しかし実際の市場ではボラティリティは時とともに変動し、そのことにより資産のリターンの分布は正規分布から乖離し、ファット・テイルとなる傾向があります。ファット・テイルとは分布の両極端の発生確率が正規分布と比較して大きくなる、すなわち確率密度関数の裾野が正規分布より高くなる事象です。このことは標準偏差の異なる正規分布を重み付けして足し合わせた分布と、単純な正規分布を比較してみることで理解することができます。
一般的なボラティリティの推定方法
オプション評価やリスク定量化のモデルにおいては、一般的に資産のリターンが正規分布に従うと仮定されます。ボラティリティとは資産価格の変動の大きさの指標ですが、リスク管理の実務においては、一般的にボラティリティは日次リターンの標準偏差として定義されています。ボラティリティの推定にあたって、まず日次の資産価格の過去データから、日次リターンの時系列データを作成します。
![]()
(60.1)
ただし、
Si : 日付iにおける資産Sの価格
ri : 日付iにおける資産Sの日次リターン
日次リターンの時系列データから、次の式によってボラティリティを推定します。
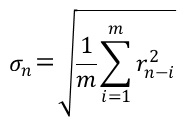
(60.2)
ただし、
σn : 日付nにおける推定ボラティリティ(標準偏差)
m : ボラティリティ推定に用いる時系列データの日数
注: (60.2)は厳密なものではなく、実務的に用いられる簡略化した式となります。
(60.2)式の両辺を二乗して展開すると以下のようになります。
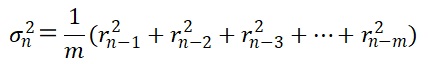
(60.3)
この式の意味するところは、m日間の日次リターンの二乗の平均値が日次リターンの分散(標準偏差の二乗)であるとして、ボラティリティを推定しているということになります。
使用するデータ期間(m日)の設定には注意が必要です。期間が長いほど、より古いデータも使用することになりますが、現在のボラティティリティを推定するのに、古いデータは現在の市場の状況に合わない場合も考えられ、信頼性が低くなります。一方で期間を短くすると、使用するデータ数が少ないために推定値が正確でなくなる恐れがあります。真の値と推定値の誤差の標準偏差のことを標準誤差と言いますが、データ数(m日)が多いほど標準誤差は小さくなります。
指数加重移動平均法(指数平滑化法)による推定
このデータ期間の設定における問題に対処する方法の一つに指数加重移動平均法(あるいは指数平滑化法と呼ばれる)があり、実務的にもよく用いられています。
(60.3)式においてはm日前から前日まで、どのデータも均等に1/mの同じ重み付けとなりますが、指数加重移動平均法においては、日数を遡るにつれ重み付けが逓減します。具体的には直近データ r2n-1 のウェイトを w0 とした場合、その1日前のデータ r2n-2 のウェイトはλ倍(ただし0<λ<1)の w0λとします。さらに1日前のデータ r2n-3 のウェイトはそのさらにλ倍の w0λ2 とし、以下同様です。
![]()
(60.4)
この手法の特徴は、ボラティリティ推定に用いるデータ数を減らすことなく、重み付けにより、新しいデータの影響を古いデータよりも大きくする点です。
ウェイトの合計は1なので、無限等比級数の和の公式を利用して、w0を求められます。
![]()
(60.5)
(60.4)式と(60.5)式から、日付nにおけるボラティリティは下式のように推定されます。
![]()
(60.6)
また、同様に日付n-1におけるボラティリティは下式のように推定されます。
![]()
(60.7)
(60.7)式を(60.6)式に代入すると、下式が得られます。
![]()
(60.8)
(60.8)式は、指数加重移動平均法のもう一つの特徴として、日付nにおけるボラティリティは、日付n-1における推定ボラティリティと、日付n-1におけるリターンのみから推定されることを示しており、言い換えると推定ボラティリティの日次更新の際に、ヒストリカルの日次リターンデータは必要ないということになります。
λの推定
指数加重移動平均法のウェイトの逓減速度のパラメーターであるλは、大きすぎると新しいデータのウェイトが低くなり直近の市場変動の反映が遅くなり、逆に小さすぎると推定ボラティリティは不安定になりがちです。λの推定には、モデルが予想したボラティリティと、実現したボラティリティを比較して、誤差を最小にするλを求める方法や、観測データから最尤推定により求める方法等があります。ご参考までに、1990年代JPモルガンのリスク・メトリックスにおいては、全市場共通のλとして0.94が採用されていました。
ヒストリカルシ・ミュレーション
指数加重移動平均法の考え方はバリュー・アット・リスク(以下「VaR」)や期待ショートフォール(以下「ES」)等のリスク指標の推定にも応用することが可能です。一般的な手法においては過去のサンプル期間の観測データは均等に重み付けされますが、観測データを重み付けして、新しいデータの影響を古いデータより大きくすることが可能ですが、実務的にはリスク指標の安定性を重視して、均等ウェイトが採用されているケースが多いと考えられます。
【参考文献】
・Valuation and Risk Models (Pearson Education) 等
◇MRAフェロー 伊東啓介
