リスク管理最前線 第52回 〜市場リスク指標の推定(パート5)テール・リスク定量化の統計学的アプローチ〜
- 欧米金融機関の現場から
- リスク管理コラム
- リスク管理最前線
市場リスク指標の推定(パート5)テール・リスク定量化の統計学的アプローチ
発現することが極めて稀ですが、発現した際には非常に大きな損失を被りうるような、経済危機や甚大な自然災害等の極端なイベントは、リスク管理において大変重要なテーマです。企業経営においては、ある程度極端なイベントが発生しても破綻を回避するために必要な自己資本の額を決定することは経営の健全性に関わる重要な問題ですし、公共の災害対策では海岸や河川の堤防の高さをどのぐらいにするかはやはり人命や安全性に関わる重要な問題です。
しかしバリュー・アット・リスク(VaR)等の手法で推定する一定の信頼水準での損失額をはるかに超えるような「極端なイベント」の影響を定量化することは大変な困難を伴います。発現することが稀なため、観測できる事象が非常に少ないからです。そのため様々な仮定を置いて推定を試みることになりますが、そのような仮定が適切なのかどうかも本当のところは分かりません。リスク管理に絶対は無く、どんなに対策を施しても想定外の事象は発生し得るものですが、影響が非常に大きいため、その限界を理解した上で、定量化する試みは不可欠です。
統計学の世界で極値理論(あるいはEVT。Extreme Value Theoryの略)と呼ばれる考え方があり、リスクの最大値の分布や閾値の超過分布について、その特徴を分析することにより「極端なイベント」のリスク評価に活用することが可能です。今回は極値理論を活用した「極端なイベント」の影響(以下「テール・リスク」と呼ぶ)の定量化手法の概要についてご紹介します。
一般化極値理論 (GEV)
ある損失データの変数をXとして、Xが独立同一分布(個別の標本(サンプル)が、他の標本の値に関係なく独立に得られる、またそれらの標本が同じ確率分布から得られるという条件を満たす分布)に従う場合にXの極値を推定することが目的となりますが、Xが従う確率分布をF(x)とすると、具体的にF(x)がどのような分布かは分かっていません。ここでF(x)からn個のデータを抽出した場合の最大値をMnとすると、nが十分大きな値であればMnは極値とみなすことができますが、nが十分大きくなるとMnは一般化極値(「GEV」と呼ばれる。General Extreme Valueの略)分布というある特定の確率分布に従うということが、Fisher-Tippett-Gdenenkoの定理から分かっています。元のデータXの従う確率分布が不明でも、極値Mnの従う確率分布が分かるというのが驚くべきことなのですが、この事実はテール・リスクの定量化に好都合です。数式で示すと、 Mnの分布は以下の一般化極値(GEV)分布に収束します。
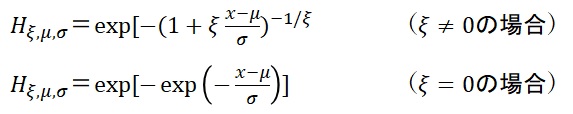 ただし、
ただし、
μ : 位置 (location) パラメータ。Mnの中心傾向の指標
σ:スケール (scale) パラメータ。Mnの分散度合いの指標
ξ :形状 (shape) パラメータ。Mnのテールの形状の指標
さらにGEVは、ξ の値により、3種類のいずれかの分布になります。
ξ>0 の場合:フレッシェ分布 (Frechet)
ξ=0 の場合:グンベル分布 (Gumbel)
ξ<0 の場合:ワイブル分布 (Weibull)
詳細な説明は割愛しますが、分布のテールが厚い(分布の裾野、すなわち極値の確率密度が高い)順に、フレッシェ分布、グンベル分布、ワイブル分布となります。
関数の形が分かったとは言え、確率分布の決定にはパラメータの推定が必要となります。これにもいくつかの手法がありますが、代表的なものとしては、最尤推定法、回帰分析法、セミパラメトリック推定法があります。詳細には立ち入りませんが、結局のところパラメータを数の少ない観測値に合わせていく必要があり、信頼性にはどうしても限界があると言わざるを得ません。
最終的に極値の分布関数が決定されると、極値のパーセンタイル値や、一定の信頼水準でのレンジを推定することが可能となります。
閾値超過の極値理論
一般化極値理論(GEV)においては多数の観測値の中からサンプルの最大値Mnのみに着目するため、多くの観測データを使用しないことになります。そこで一定の閾値を超過するデータを全て利用して統計分析する手法が研究されました。一定の閾値を超過するデータの分布は、以下の一般化パレート(Generalized Pareto)分布に収束することが、Gdenenko-Pickands-Balkema-deHaan (GPBdH) の定理により分かっています。
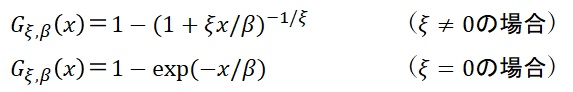 ただし、
ただし、
β:スケール (scale) パラメータ。閾値超過データの分散度合いの指標
ξ :形状 (shape) パラメータ。閾値超過データのテールの形状の指標
一般化極値理論との比較においては、より多くのデータを利用することに加えて、推定パラメータが一つ少ないということも利点です。ただし閾値の設定をどうするかという問題があり、データの特性等にもよって、必ずしも一般化パレート分布が一般化極値分布(GEV)より取り扱いやすいとは言えません。どちらを利用するかはデータの特性や目的によって判断することになります。
多変数の極値理論
「極端なイベント」を考える場合に、実際には複数のリスクファクターがあり、多変数の分布の極値が収束する分布を扱う必要が生じますが、その際にはコピュラを利用することになります。コピュラとは統計学において多変数の累積分布関数とその周辺分布関数の関係を示す関数のことですが、多変数の分布を1変数の分布にコピュラで分解し、1変数の分布の最大値が収束する分布を求めた後、再度コピュラで結合することにより、多変数の分布の最大値が収束する分布を求めることが可能です。ただし変数が増加するにつれ、取り扱いの複雑さや推定するパラメータの数が増すという問題に加え、多変数が同時に極値を取る確率は極端に低下するという特徴にも留意が必要です。また各変数のテール・リスクが独立事象であるというモデルの前提が、実際には成立しない場合が多いという点に注意が必要です。経験的に一つの極端なイベントが引き金となって、別の極端なイベントを引き起こすという事実はよく知られています。
極値理論に関する結論
極値理論は元データの分布を特定せずとも極値に適用できるモデルという大きな利点があり、比較的単純なケースにおいてはその威力を発揮します。しかし極値の特性ではありますが、信頼区間は広くなりがちで、推定が容易ではないモデルパラメータに依存する不確実性の問題があります。しかし観測数の極めて少ない極値の推定においては他に良い方法が存在するわけではなく、その限界を理解した上で極値理論を活用するしかないと一部の専門家の間では考えられています。
最後にテール・リスクの定量化においては統計学的なアプローチとは全く異なりますが、発現した場合の影響度合いを推定するという目的において、リスク管理の実務的にはストレス・テストが用いられています。ストレス・テストについては過去の本コラムでも何度か紹介しています。
【参考文献】
損保総研レポート第92号 「極値事象のリスク管理」
Market Risk Management and Measurement (Pearson Education) 等
◇MRAフェロー 伊東啓介
