リスク管理最前線 第27回 〜バリュー・アット・リスク実践編 分散共分散法〜
- リスク管理最前線
- 欧米金融機関の現場から
- リスク管理コラム
バリュー・アット・リスク実践編 分散共分散法
以前本コラムにおいてバリュー・アット・リスク(以下「VaR」)の意義や推定方法について概略をご紹介いたしましたが、実践編として、VaR推定の手法を、実務家の視点からもう少し詳しくご紹介したいと思います。今回は実用化されているモデルの中では、VaRの黎明期から使用され、最も簡便な分散共分散法をご紹介いたします。
ポイント1:VaRとは
ポイント2:VaRの利用目的
ポイント3:分散共分散法によるVaR計測手法
ポイント4:ボラティリティと相関係数の推定手法
ポイント5:分散共分散法の弱点
ポイント6:他のリスク計測手法の併用
ポイント1:VaRとは
VaRとはあるポートフォリオが一定の保有期間(例えば1日後。以後簡略化のため「翌日」と表現する。)に被る可能性のある、最大損失額のことです。最大損失額とはポートフォリオの現在価値と、翌日の最悪ケースの価値との差額として定義されます。
ここで最悪ケースとは何かと言うと、ポートフォリオの翌日の価値がある確率分布に従うと仮定して、ある信頼区間の値を最悪ケースと定めるものです。信頼区間は目的に応じて、5%や1%等が用いられます。
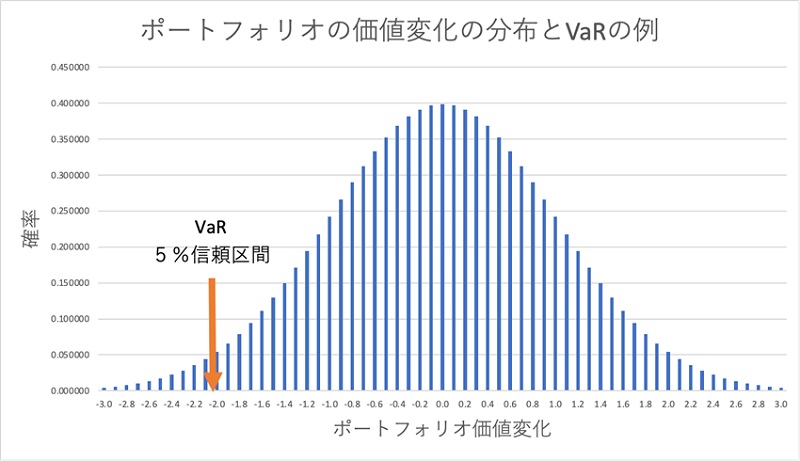
ポイント2:VaRの利用目的
VaRの主な利用目的として、自己資本、あるいは自己資本内で経営が定めるリスク許容度の範囲内にリスクをコントロールすることが挙げられます。逆にあるポートフォリオを保有する際に、引当金や追加資本がどの程度必要になるかを計測する手段にもなり得ます。また各ビジネスのリスク・リターンのパフォーマンスの測定や比較に利用されることもあります。
ポイント3:分散共分散法によるVaR計測手法
ステップ1:例えば株式であれば、各銘柄の保有額を把握。
ステップ2:各銘柄の最悪ケースの動きを観測。
① 分散共分散法では各資産が正規分布や対数正規分布等、特定の分布に従うと仮定します。例えば金利は正規分布、株式のように負の値をとらないものは対数正規分布等を用います。
② 分布のボラティリティ(σ)はヒストリカルデータから推定します。
③ これらの仮定から、求める信頼区間に対応する変化幅あるいは変化率を求めます。正規分布であれば片側5%信頼区間は分布の性質から1.65xボラティリティで算出できます。
ステップ3:各資産の最大損失額の推定。保有額X最悪ケースの変化率 (または感応度X最悪ケースの変化幅) により各資産の最大損失額を推定。
ステップ4:各資産間の相関係数マトリックスを使用して、ポートフォリオ全体の最大損失額を推定。相関係数マトリックスもボラティリティ同様ヒストリカルデータより推定。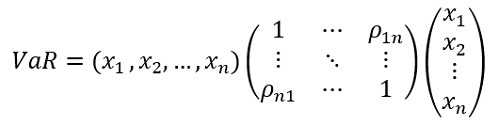
ポイント4:ボラティリティと相関係数の推定手法
前述のとおり、ヒストリカルデータを使用しますが、データ期間は短期間だとデータが少なすぎますし、長期間すぎると古いデータが多くなり、近い将来のパラメーター推定には向かないかもしれませんので、通常6ヶ月間から長くとも2、3年間程度の期間のデータを使用します。また各データサンプルを均等に扱うのではなく、より新しいデータに重み付けする方法を使う方法もあります。
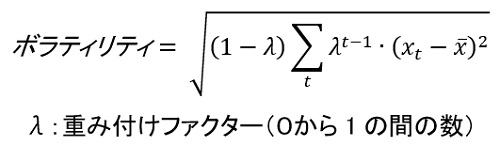
相関係数についてもボラティリティと同様の手法で推定します。ρ12=σ12/(σ1∙σ2 )の関係式から、共分散、標準偏差のデータから導きます。(ρ12:相関係数、σ12:共分散、σ1、σ2:標準偏差(ボラティリティ))
ポイント5:分散共分散法の弱点
オプション等原資産化価格の変化に対して価値変化が非線形の場合、原資産価格に対する一次的なリスク(デルタ)のみ考慮して、二次的なリスク(ガンマ)を考慮できていない(注)ため、誤差が生じる場合があります。なおボラティリティに対する一次的なリスク(ベガ)に関しては分散共分散法のモデルの枠組みで取り扱うことができます。(注:理論的には二次項まで考慮するモデルは可能だが、煩雑なため通常実装されない。)
またいくつかのモデルの仮定は必ずしも正しいものではありません。例えば変化の分布形の仮定や、過去データから将来を推定できると仮定することは、往々にして現実と異なる場合があります。
ポイント6:他のリスク計測手法の併用
分散共分散法はリスクが線形なポートフォリオにおいて簡便で有力な手法ではありますが、上述の弱点を補うため、他の手法によるVaRを併用することが有効です。ヒストリカル・シミュレーションやモンテカルロ・シミュレーション法が代表的な代替手法です。
またストレス・テストがポートフォリオの複雑化に伴いより重要性を増しており、VaRと併用することが重要であり一般的となっています。
◇MRAフェロー 伊東啓介
