リスク管理最前線 第69回 〜債券市場分析（パート１）スポットレートとディスカウントファクター、イールドカーブ〜
- 欧米金融機関の現場から
- リスク管理コラム
- リスク管理最前線
債券市場分析（パート１）スポットレートと
ディスカウントファクター、イールドカーブ
今回から債券市場分析において必要となる基礎的な概念や手法についてご紹介したいと思います。初回はスポットレートとディスカウントファクターについてです。スポットレートとは将来のキャッシュフローを現在価値に割り引く時の利率（レート）で、割引率とも呼ばれます。ディスカウントファクターとは将来のキャッシュフローの現在価値を求めるための係数です。日本の国債市場を例に債券の価格からスポットレート及びディスカウントファクターを求める方法及び両者の関係について説明し、金利の期間構造であるイールドカーブの基本的な作成手順を示します。
短期国債（TB）
日本における短期国債は、満期が1年以内の割引債で、3ヶ月物、6ヶ月物、1年物等が金融機関や機関投資家向けに発行されています。割引債とは利払いがなく、満期に額面で払い戻される債券です。通常発行価格が額面を下回り、見方を変えると額面と発行価格の差額が利子に相当すると言えます。
割引債のキャッシュフローは図1のとおりです。
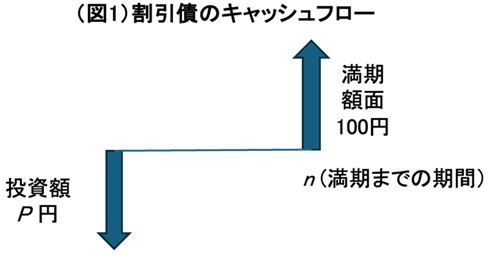
割引債価格とスポットレート
満期までの残存期間がn年の額面100円の割引債のスポットレート（年率）をrとすると、割引債の価格Pは、
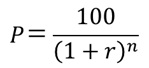
(69.1)
と表せます。なお、（69.1）式のとおり、スポットレートは割引債のように、投資時点と満期時点のみにキャッシュフローが発生する時の複利最終利回りとして定義されるため、ゼロ・クーポン・レートとも呼ばれます。
例えば満期まで3ヶ月の割引債のスポットレートレートが0.40%である場合、価格は
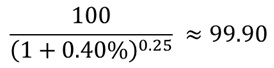
となります。
また (69.1)式を変形すると、
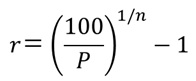
(69.2)
となり、満期までn年の額面100円の割引債の価格Pがわかっている場合、スポットレートrを計算することができます。
例えば満期まで3ヶ月の額面100円の割引債の価格が99.95円である場合、スポットレートは、
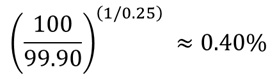
と求められます。
割引債価格とディスカウントファクター
ディスカウントファクターとは前述のとおり将来のキャッシュフローの現在価値を求める係数ですが、n年のディスカウントファクターDFnは、n年後のキャッシュフロー 1単位の現在価値を表します。
額面100円、満期までn年の割引債の価格（＝現在価値）がP円である場合、割引債のキャッシュフローはn年後に受け取る100円のみなので、
(69.3)
という関係が成り立ちます。これを変形すると、
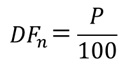
(69.4)
となり、割引債の価格から直接ディスカウントファクターが求められることがわかります。
例えば満期まで残存期間3ヶ月の額面100円の割引債の価格が99.90円である場合、3ヶ月のディスカウントファクターDF0.25は、0.9990となります。同様に満期の異なる割引債の価格から、各満期時点のディスカウントファクターを表1のように求めることができます。
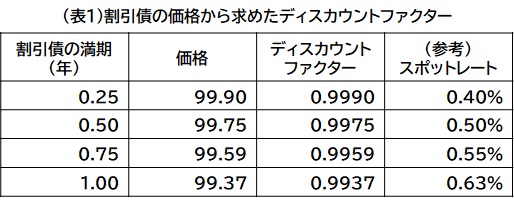
ディスカウントファクターとスポットレート
(69.1)式および（69.4）式から、
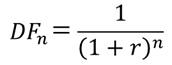
(69.5)
が導かれます。スポットレートはディスカウントファクターから算出されることが示され、その逆もまた然りです。
固定利付国債
日本における国債のうち、半年ごとに利子が支払われる利付国債には、固定利付型（決まった額の利子が支払われるタイプ）と変動利付型（利子額が変動するタイプ）があります。固定利付債には、満期が2年、5年、10年、20年、30年、40年のものがあります。固定利付債のキャッシュフローは図2のとおりです。
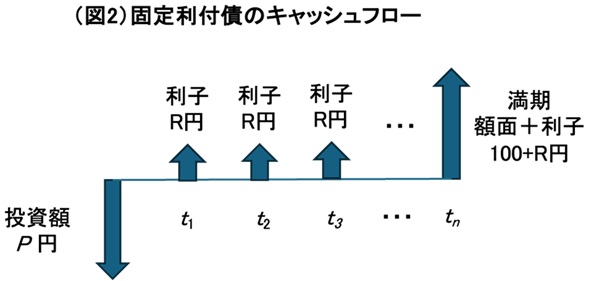
固定利付債価格とディスカウントファクター
満期までの残存期間がn年の額面100円の固定利付債の価格Pは、債券の全てのキャッシュフローをスポットレートで割り引いた現在価値の総和となります。図2の例では、
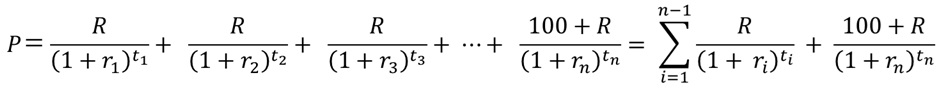(69.6)
ただし、
ri : 期間tiのスポットレート
となります。また (69.5)式から、ディスカウントファクターを使って(69.6)式を表すと、
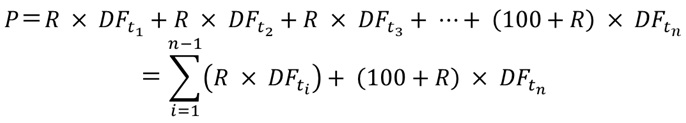
(69.7)
となります。
ブートストラッピングによるディスカウントファクターカーブ及びイールドカーブの作成
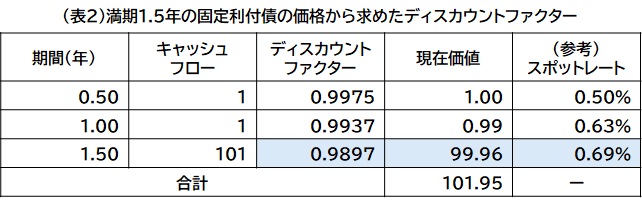
例えば残存期間1.5年、半年毎の利子が1円の固定利付債の価格が101.95円である場合、（表1）から0.5年と1.0年のディスカウントファクターはそれぞれ0.9975及び0.9937とすでに求められているので、（69.7）式に既知の値を代入すると、
となり、DF1.5=0.9897 と求められます。また、（69.5）式から1.5年のスポットレートは0.69%と求められます。（表2）
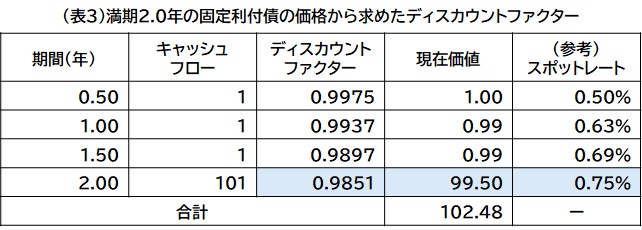
次に、残存期間2.0年、半年毎の利子が1円の固定利付債の価格が102.48円である場合、（表2）から0.5年、1.0年、1.5年のディスカウントファクターはそれぞれ0.9975、0.9937、0.9897とすでに求められているので、（69.7）式に既知の値を代入すると、
となり、DF2.0=0.9851 と求められます。また、（69.5）式から2.0年のスポットレートは0.75%と求められます。（表3）
同様に、満期の近い固定利付債の価格から順番に、満期のディスカウントファクターを求めることが可能ですが、この手法はブートストラッピングと呼ばれます。ブートストラッピングにより作成されるディスカウントファクターの期間構造はディスカウントファクターカーブ、また、スポットレートの期間構造はイールドカーブと呼ばれます。
【参考文献】
・Valuation and Risk Models: Global Association of Risk Professionals
・スポットレートとその応用（日本銀行金融機構局金融高度化センター）
・財務省ホームページ他
◇MRAフェロー 伊東啓介